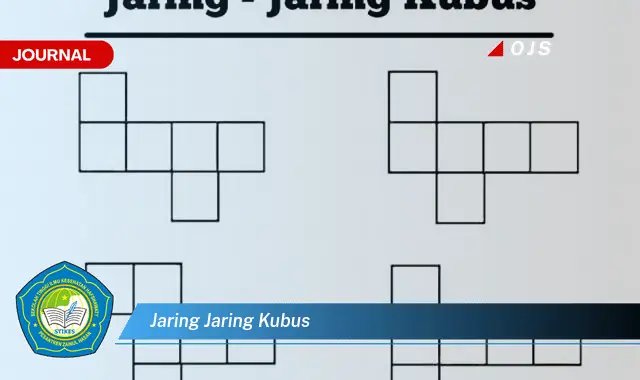
Jaring-jaring kubus adalah bangun datar dua dimensi yang jika dibentuk dan dihubungkan sesuai dengan aturannya akan membentuk bangun ruang tiga dimensi yang disebut kubus. Jaring-jaring kubus terdiri dari enam bidang persegi yang sama dan kongruen.
Jaring-jaring kubus memiliki beberapa sifat penting, seperti:
- Memiliki enam bidang berbentuk persegi.
- Memiliki dua belas rusuk yang sama panjang.
- Memiliki delapan titik sudut.
Jaring-jaring kubus memiliki banyak kegunaan dalam kehidupan sehari-hari, seperti:
- Sebagai kerangka dasar dalam pembuatan benda-benda tiga dimensi, seperti kotak, lemari, dan rumah.
- Sebagai bahan dasar dalam pembuatan origami.
- Sebagai alat bantu dalam pembelajaran geometri.
Selain itu, jaring-jaring kubus juga memiliki nilai historis. Bangun ini ditemukan oleh bangsa Mesir Kuno sekitar tahun 3000 SM dan digunakan sebagai dasar pembangunan piramida.
Selanjutnya, kita akan membahas topik-topik utama yang berkaitan dengan jaring-jaring kubus, seperti cara menggambar, menghitung luas permukaan, dan volume kubus yang terbentuk.
Jaring-Jaring Kubus
Jaring-jaring kubus merupakan aspek penting dalam memahami bangun ruang kubus. Berikut lima aspek penting yang terkait dengan jaring-jaring kubus:
- Bentuk: Enam bidang persegi
- Sisi: Dua belas rusuk sama panjang
- Sudut: Delapan titik sudut
- Luas Permukaan: Jumlah luas keenam bidang persegi
- Volume: Hasil perkalian panjang, lebar, dan tinggi kubus yang terbentuk
Memahami aspek-aspek ini sangat penting untuk menguasai konsep jaring-jaring kubus. Sebagai contoh, mengetahui bentuk jaring-jaring kubus memudahkan kita dalam menggambar dan mengenalinya. Mengetahui jumlah sisi dan sudut membantu kita dalam menghitung dan menganalisis sifat-sifat kubus. Memahami luas permukaan dan volume kubus sangat penting dalam aplikasi praktis, seperti menghitung kebutuhan bahan dan merencanakan konstruksi.
Bentuk
Bentuk jaring-jaring kubus yang terdiri dari enam bidang persegi merupakan aspek krusial yang menentukan sifat-sifat kubus yang terbentuk. Enam bidang persegi ini saling berpotongan pada rusuk-rusuknya, membentuk sudut siku-siku di setiap titik potongnya.
Struktur enam bidang persegi ini sangat penting karena memberikan kekokohan dan stabilitas pada kubus. Jika jaring-jaring kubus memiliki bentuk selain persegi, seperti segitiga atau lingkaran, maka kubus yang terbentuk akan memiliki struktur yang tidak stabil dan mudah berubah bentuk.
Selain itu, bentuk persegi pada jaring-jaring kubus memudahkan dalam proses penggambaran, pembuatan model, dan perhitungan. Sifat-sifat persegi, seperti memiliki empat sisi yang sama panjang dan empat sudut siku-siku, menyederhanakan berbagai operasi matematika yang terkait dengan kubus.
Oleh karena itu, bentuk jaring-jaring kubus yang terdiri dari enam bidang persegi menjadi dasar penting dalam memahami sifat-sifat kubus dan penerapannya dalam berbagai bidang.
Sisi
Dua belas rusuk sama panjang merupakan salah satu aspek penting dari jaring-jaring kubus. Rusuk-rusuk ini menghubungkan keenam bidang persegi yang membentuk jaring-jaring kubus.
Kesamaan panjang rusuk sangat penting untuk memastikan bahwa kubus yang terbentuk memiliki bentuk yang teratur dan simetris. Jika panjang rusuk berbeda-beda, maka kubus yang dihasilkan akan menjadi tidak beraturan dan tidak stabil.
Selain itu, dua belas rusuk sama panjang berperan penting dalam menentukan sifat-sifat kubus, seperti luas permukaan dan volume. Panjang rusuk menjadi faktor pengali dalam perhitungan luas permukaan dan volume, sehingga akurasi panjang rusuk sangat memengaruhi hasil perhitungan.
Jadi, dua belas rusuk sama panjang pada jaring-jaring kubus merupakan komponen penting yang menentukan bentuk, kestabilan, dan sifat-sifat kubus yang terbentuk.
Sudut
Delapan titik sudut pada jaring-jaring kubus merupakan aspek penting yang menentukan bentuk dan sifat kubus yang akan dibentuk. Titik sudut ini merupakan titik pertemuan dari tiga rusuk kubus.
-
Menentukan Bentuk Kubus
Titik sudut berperan penting dalam menentukan bentuk kubus. Delapan titik sudut yang tersusun secara teratur membentuk kerangka dasar kubus dan memastikan bentuknya yang simetris dan kokoh. -
Kekuatan dan Stabilitas
Titik sudut pada jaring-jaring kubus memberikan kekuatan dan stabilitas pada kubus yang terbentuk. Struktur sudut siku-siku pada titik sudut memastikan distribusi beban yang merata dan mencegah kubus dari deformasi. -
Penghitungan Volume
Titik sudut menjadi faktor penting dalam penghitungan volume kubus. Panjang diagonal ruang kubus, yang menghubungkan dua titik sudut yang berhadapan, digunakan untuk menghitung volume kubus. -
Penerapan dalam Kehidupan Nyata
Prinsip titik sudut pada jaring-jaring kubus banyak diterapkan dalam kehidupan nyata, seperti pada konstruksi bangunan, desain furnitur, dan pembuatan kemasan.
Dengan demikian, delapan titik sudut pada jaring-jaring kubus merupakan komponen penting yang menentukan bentuk, kekuatan, stabilitas, dan penerapan kubus dalam berbagai bidang.
Luas Permukaan
Luas permukaan jaring-jaring kubus merupakan aspek penting yang menentukan sifat dan kegunaan kubus yang akan dibentuk. Luas permukaan dihitung dengan menjumlahkan luas keenam bidang persegi yang menyusun jaring-jaring kubus.
Luas permukaan jaring-jaring kubus sangat penting karena beberapa alasan:
- Kekuatan dan Stabilitas: Luas permukaan yang lebih besar memberikan kekuatan dan stabilitas yang lebih baik pada kubus yang terbentuk. Struktur yang lebih luas dapat menahan beban yang lebih besar dan mencegah deformasi.
- Penggunaan Bahan: Luas permukaan menentukan jumlah bahan yang dibutuhkan untuk membuat kubus. Perhitungan yang tepat dari luas permukaan sangat penting untuk memastikan penggunaan bahan yang efisien.
- Aplikasi Praktis: Luas permukaan menjadi faktor penting dalam berbagai aplikasi praktis, seperti pengemasan, konstruksi, dan desain interior. Mengetahui luas permukaan memungkinkan perencanaan dan optimalisasi yang lebih baik.
Oleh karena itu, luas permukaan jaring-jaring kubus merupakan komponen penting yang menentukan sifat fisik, penggunaan bahan, dan aplikasi praktis kubus dalam berbagai bidang.
Volume
Volume merupakan besaran yang menyatakan banyaknya ruang yang ditempati oleh suatu benda tiga dimensi. Dalam konteks jaring-jaring kubus, volume merupakan hasil perkalian dari panjang, lebar, dan tinggi kubus yang terbentuk.
-
Perhitungan Volume
Volume kubus dapat dihitung dengan mengalikan panjang, lebar, dan tinggi kubus. Ketiga besaran ini dapat diperoleh dari pengukuran rusuk-rusuk jaring-jaring kubus. -
Aplikasi Praktis
Perhitungan volume kubus sangat penting dalam berbagai aplikasi praktis, seperti:- Arsitektur dan konstruksi: Menghitung volume ruang sebuah bangunan atau kapasitas tangki air.
- Industri kemasan: Menentukan volume kemasan yang dibutuhkan untuk produk tertentu.
- Transportasi: Menghitung volume ruang kargo pada kendaraan.
-
Sifat Kubus
Volume kubus bergantung pada panjang rusuknya. Kubus dengan rusuk yang lebih panjang akan memiliki volume yang lebih besar. -
Hubungan dengan Jaring-jaring Kubus
Jaring-jaring kubus menyediakan informasi tentang rusuk-rusuk kubus yang akan dibentuk. Dengan mengukur dan menghitung panjang rusuk-rusuk tersebut, kita dapat menentukan volume kubus menggunakan rumus perhitungan volume.
Dengan demikian, pemahaman tentang volume kubus melalui jaring-jaring kubus sangat penting dalam berbagai bidang aplikasi praktis dan teoretis.
Pertanyaan Umum tentang Jaring-Jaring Kubus
Berikut adalah beberapa pertanyaan umum seputar jaring-jaring kubus beserta jawabannya:
Pertanyaan 1: Apa itu jaring-jaring kubus?
Jawaban: Jaring-jaring kubus adalah bangun datar dua dimensi yang jika dibentuk dan dihubungkan sesuai aturannya akan membentuk bangun ruang tiga dimensi yang disebut kubus.
Pertanyaan 2: Berapa jumlah bidang pada jaring-jaring kubus?
Jawaban: Jaring-jaring kubus memiliki enam bidang berbentuk persegi yang sama dan kongruen.
Pertanyaan 3: Apa saja sifat-sifat jaring-jaring kubus?
Jawaban: Jaring-jaring kubus memiliki sifat-sifat berikut: memiliki enam bidang berbentuk persegi, memiliki dua belas rusuk yang sama panjang, dan memiliki delapan titik sudut.
Pertanyaan 4: Apa saja kegunaan jaring-jaring kubus?
Jawaban: Jaring-jaring kubus memiliki banyak kegunaan, seperti sebagai kerangka dasar dalam pembuatan benda-benda tiga dimensi, sebagai bahan dasar dalam pembuatan origami, dan sebagai alat bantu dalam pembelajaran geometri.
Dengan memahami konsep jaring-jaring kubus dan sifat-sifatnya, kita dapat mengaplikasikannya dalam berbagai bidang kehidupan.
Selanjutnya, kita akan membahas topik-topik utama yang berkaitan dengan jaring-jaring kubus, seperti cara menggambar, menghitung luas permukaan, dan volume kubus yang terbentuk.
Tips Memahami Jaring-Jaring Kubus
Memahami jaring-jaring kubus merupakan dasar penting dalam geometri dan memiliki berbagai aplikasi praktis. Berikut adalah beberapa tips untuk membantu Anda memahami konsep ini dengan lebih baik:
Tip 1: Visualisasikan Kubus
Bayangkan jaring-jaring kubus sebagai kerangka dasar kubus tiga dimensi. Hal ini akan membantu Anda memahami bagaimana bidang-bidang persegi terhubung dan membentuk kubus.
Tip 2: Pahami Sifat Kubus
Pelajari sifat-sifat kubus, seperti memiliki enam bidang persegi, dua belas rusuk sama panjang, dan delapan titik sudut. Memahami sifat-sifat ini akan membantu Anda mengidentifikasi dan menggambar jaring-jaring kubus dengan benar.
Tip 3: Latihan Menggambar
Berlatihlah menggambar jaring-jaring kubus dari berbagai sudut pandang. Hal ini akan meningkatkan pemahaman Anda tentang bagaimana bidang-bidang terhubung dan bagaimana kubus akan terbentuk.
Tip 4: Gunakan Alat Bantu
Gunakan alat bantu seperti penggaris, jangka, dan kertas berpetak untuk menggambar jaring-jaring kubus yang akurat. Alat bantu ini akan memastikan bahwa bidang-bidang dan rusuk memiliki ukuran dan proporsi yang benar.
Tip 5: Terapkan dalam Kehidupan Nyata
Cobalah terapkan konsep jaring-jaring kubus dalam kehidupan nyata, seperti membuat kerangka kubus dari kertas atau kardus. Hal ini akan membantu Anda memahami aplikasi praktis dari jaring-jaring kubus.
KesimpulanMemahami jaring-jaring kubus sangat penting untuk menguasai konsep geometri dan penerapannya dalam berbagai bidang. Dengan mengikuti tips di atas, Anda dapat meningkatkan pemahaman Anda tentang topik ini dan menggunakannya secara efektif dalam aplikasi praktis.
Youtube Video:










